DP Series - The Rod Cutting Problem

Given that selling a rod of length i yields a profit of p_i , how do we cut a rod of length n to maximize the total revenue?

Method 1: Recursion

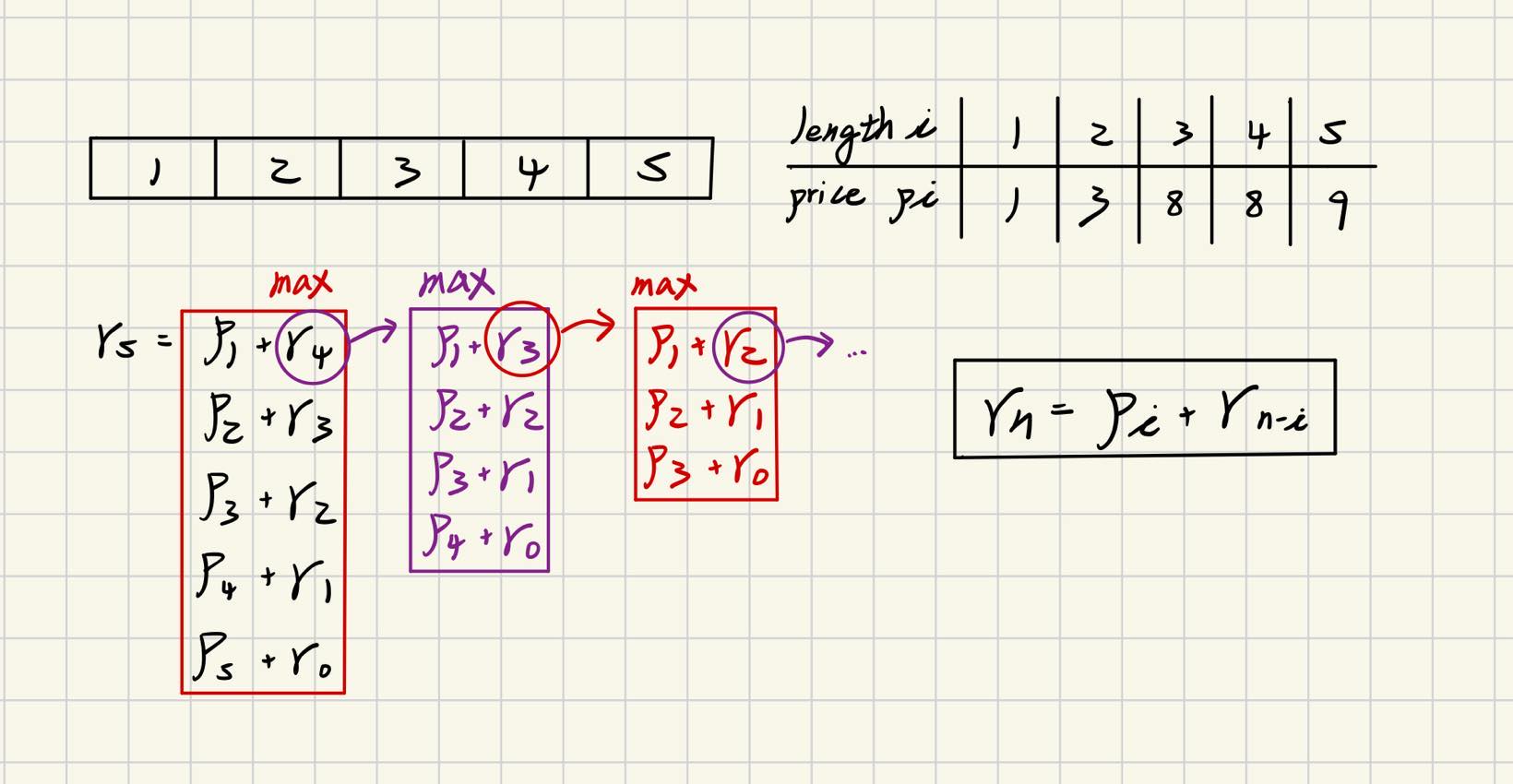
The most straightforward approach is to solve it using recursion. As shown in the figure below, r_n represents the maximum revenue obtainable by cutting a rod of length n. Suppose i is the length of the first segment in the optimal solution; then r_n = p_i + r_n−i, because p_i is the revenue from the first segment in the optimal solution, and adding the maximum revenue from the remaining part gives us the answer.

How do we find i? By looping through i from 0 to n−1, evaluating each combination p_i + r_n−i, and selecting the maximum value as the answer.

However, this approach has a problem: each time we compute r_n−i, it requires recursively calculating its optimal solution, leading to repeated calculations. For instance, when computing r₄, we need to compute r₃, r₂, r₁, r₀, and computing r₃ requires recomputing r₂, r₁, r₀. Therefore, we can use Dynamic Programming (DP) to save time.

Method 2: DP

We can build a table to store the values of each r_i, so we don’t have to recalculate them every time i is needed.

Given r₀ and r₁, we can compute r₂ as follows: r₂ = max( p₁ + r₁, p₂ + r₀ ). Next, using r₁ and r₂, we can compute r₃, and finally determine r₅. The most crucial part is still the recursive formula p_i + r_n-i.

Quick Note

Building a table to store repetitive parts in recursion is a key technique in Dynamic Programming!